검색 엔진은 어떻게 작동하는가

우리는 평소에 수많은 데이터를 찾는다. 문서가 될 수도 있고, 서비스에서 남은 로그가 될 수도 있다. 하지만 우리는 문서를 찾을 때 개발을 할 때처럼 문서를 대표하는 값(예를 들어, 문서의 고유 번호)을 통해 찾지 않는다. 대신 우리는 문서에 포함될 것이라 예상하는 단어를 통해 찾으려고 한다. 그렇다면 이런 방식의 검색은 어떻게 이루어지는 것일까? 아주 간단한 검색 엔진을 구현해 보며 검색 엔진의 기본적인 작동 원리에 대해 알아본다.

검색 엔진

먼저 검색 엔진이 하는 일을 정의 해보자. 검색 엔진이 하는 일은 간단하게 아래 세 가지로 이루어진다.

  1. 사용자에게 쿼리(검색어)를 입력받는다.
  2. 검색어와 가장 유사한 문서를 찾는다.
  3. 찾은 문서를 사용자에게 보여준다.

간단한 검색 구현하기

가장 쉽게 구현할 수 있는 검색은 바로 입력한 검색어가 완벽히 포함되는 문서를 찾는 것이다.

아래와 같이 query라는 쿼리가 doc.Content라는 문서 내용에 포함되는지 확인하면 아주 단순한 검색 기능이 완성된다.

var query string
var documents []Document

for _, doc := range documents {
  // 만약 쿼리가 문서 본문에 포함되어 있다면
  if strings.Contains(doc.Content, query) {
    // 임의의 작업을 한다. 예를 들어, 검색 결과에 이 문서를 추가한다.
  }
}
var query string
var documents []Document

for _, doc := range documents {
  // 만약 쿼리가 문서 본문에 포함되어 있다면
  if strings.Contains(doc.Content, query) {
    // 임의의 작업을 한다. 예를 들어, 검색 결과에 이 문서를 추가한다.
  }
}

예외

일단 동작은 하지만 이 방식은 여러 단어로 이루어진 쿼리가 주어진다면 사용자가 의도한 대로 문서를 찾지 못하는 문제점이 있다.

아래와 같은 경우처럼 분명히 문서에는 apple과 juice 모두 포함되어 있지만 앞선 방법대로라면 apple juice라는 문자열이 포함되었는지를 검사하기에 이 문서는 검색 결과에 포함되지 않을 것이다.

strings.Contains("red apple and orange juice", "apple juice")
strings.Contains("red apple and orange juice", "apple juice")

그렇다면 이 문제는 어떻게 해결할 수 있을까? 가장 단순하게 접근해 보면 쿼리를 공백으로 구분하여 각각의 단어가 포함되어 있는지를 검사하는 방법이 있을 것이다. 하지만 이 방법은 그렇게 좋은 방법이 아니다. 왜냐하면 너무 느리다.

예를 들어보자. 쿼리를 공백으로 나눈 QQ개의 단어, NN의 길이를 가진 문서 그리고 각 단어의 길이를 Li(i=1,2,...,Q)L_i (i = 1, 2, ..., Q)라 하자. 문자열 검색 알고리즘은 여러 가지가 있지만 대체로 빠르다고 알려진 Knuth-Morris-Pratt 알고리즘을 사용한다고 가정하자. KMP의 시간 복잡도는 문서의 길이 NN, 쿼리의 길이 MM일때 O(N+M)O(N+M)이다. 그런데 이 경우에는 쿼리가 QQ개 있으므로 총 QQ번의 검사가 필요하며 각 단어를 검사할 때는 O(N+Li)O(N + L_i) (LiL_i = 쿼리 QiQ_i의 길이)의 시간이 걸린다.

결과적으로 매 문서 검색마다 O(Q∗N+S)O(Q * N + S) (SS = 모든 쿼리의 길이 합)의 시간이 걸리니 문서의 양이 많아지고 길어질수록 이 방법은 좋지 못하다.

데이터베이스의 힘을 빌리기

대부분의 경우 데이터베이스에 검색할 문서가 저장되어 있으므로 데이터베이스의 기능을 사용하면 보다 빠르고 간편하게 문제를 해결할 수 있다. (앞선 예시는 글의 전개를 위한 것이며 현실적이지 못하다.)

데이터베이스를 사용한다면 여러 방법으로 접근할 수 있다. 우선 가장 익숙할 SQL 패턴 매칭을 사용하는 방법이 있다.

-- LIKE
SELECT ... FROM documents WHERE text LIKE '%apple juice%'

-- REGEXP
SELECT ... FROM documents WHERE text REGEXP '.*apple juice.*'
-- LIKE
SELECT ... FROM documents WHERE text LIKE '%apple juice%'

-- REGEXP
SELECT ... FROM documents WHERE text REGEXP '.*apple juice.*'

LIKE 검색의 경우 와일드카드 % 위치에 따라 인덱스를 사용할 수도 있지만 우리가 원하는 것은 쿼리가 문서의 어느 위치에 있던 찾는 것이기에 %쿼리%와 같은 형태의 LIKE 조건은 인덱스를 사용하지 않는다. 또한 정규식 패턴 매칭은 인덱스를 사용할 수 없다.

그래서 최근 버전의 데이터베이스들은 텍스트 검색을 위한 FULLTEXT 인덱스를 제공한다. 이 인덱스를 사용하면 더 빠르게 검색할 수 있다. 실제로 앞선 방법들에 비하면 비교가 안 될 정도로 빠르며 대부분의 경우에 원하는 성능으로 검색이 가능하다.

-- FULLTEXT INDEX + MATCH .. AGAINST
CREATE TABLE documents ... text TEXT, FULLTEXT(text)
SELECT ... FROM documents WHERE MATCH(text) AGAINST('apple juice' IN BOOLEAN MODE)
SELECT ... FROM documents WHERE MATCH(text) AGAINST('apple juice' IN NATURAL LANGUAGE MODE)

-- FULLTEXT INDEX + MATCH .. AGAINST
CREATE TABLE documents ... text TEXT, FULLTEXT(text)
SELECT ... FROM documents WHERE MATCH(text) AGAINST('apple juice' IN BOOLEAN MODE)
SELECT ... FROM documents WHERE MATCH(text) AGAINST('apple juice' IN NATURAL LANGUAGE MODE)

검색을 위한 데이터베이스

MySQL이나 PostgreSQL같은 데이터베이스로도 FULLTEXT 같은 검색을 위한 인덱스 기능을 제공하지만, 검색을 잘 하지는 못한다. 예를 들면 아래와 같은 문제가 있다.

  • 약간의 오타가 있어도 검색 결과에 포함되지 않는다
  • 비정형 데이터를 처리하기 힘들다
  • 검색 결과 선정에 개입이 불가능하다
  • ...

그래서 보통 Elasticsearch나 Solr같은 검색 엔진을 사용한다. 이 엔진들은 검색을 위한 데이터베이스로서 데이터베이스의 기능을 포함하고 있으며 검색을 위한 특화된 기능들을 제공한다. 그렇다면 이렇게 빠르게 동작하는 검색 엔진들은 어떻게 동작할까? 직접 구현하면서 알아보자.

검색 엔진 구현하기

우리가 문서 검색을 하면서 가장 기본적인 관심사는 문서에 이 단어가 포함되어 있는지 알고 싶다이다. 그렇다면 어떻게 해야 앞의 문제들을 회피하면서 빠르게 문서를 탐색할 수 있을까?

인덱스 (Forward Index)

전통적인 데이터베이스를 떠올려보자. 데이터베이스는 각 문서를 대표하는 고윳값이나 여러 값들의 묶음 등을 사용하여 빠르게 문서를 찾을 수 있는 인덱스를 만든다. 그렇다면 검색 엔진에도 인덱스를 적용할 수 있지 않을까?

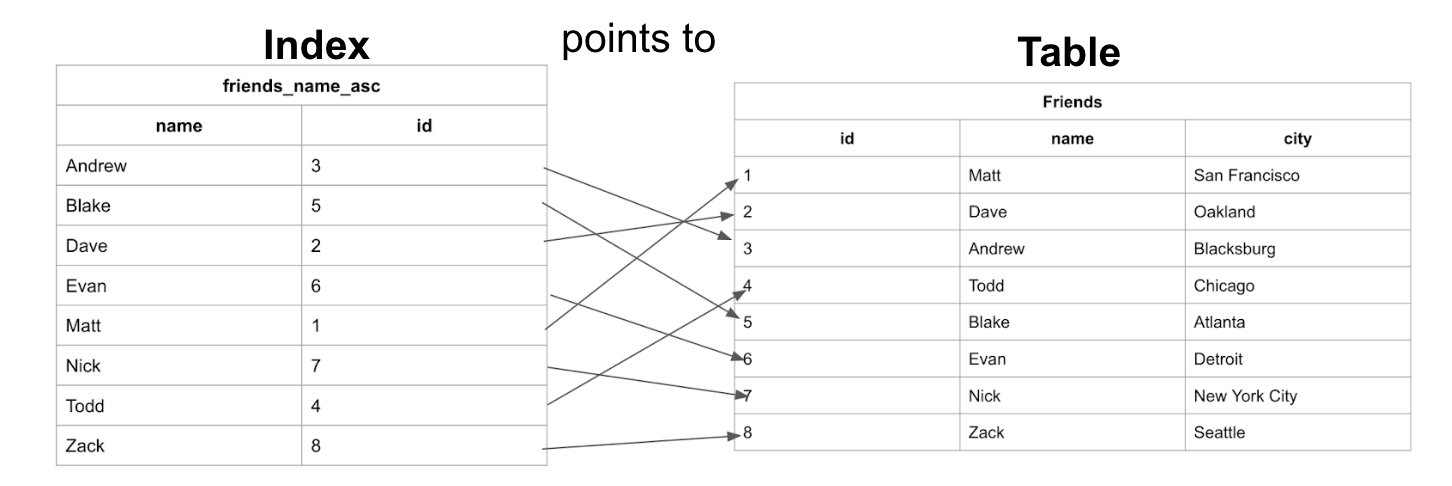
Database Index

역 인덱스 (Inverted Index)

인덱스가 각 문서가 어떤 값을 포함하고 있는지를 저장하지만 역 인덱스는 반대로 값이 어떤 문서에 포함되어 있는지를 저장한다.

아래와 같은 데이터가 있다고 가정하자.

document id text
doc1 apple favored chocolate
doc2 orange juice with candy
doc3 apple orange juice

위의 데이터를 통해 역 인덱스를 만들면 아래와 같다.

term document id
apple doc1, doc3
candy doc2
chocolate doc1
favored doc1
orange doc2, doc3
juice doc2, doc3
with doc2

역 인덱스 구현

역 인덱스를 직접 구현해 보자. 실제로 구현은 그렇게 어렵지 않다. 위의 예시대로 단어를 키로 가지고 문서의 고윳값을 배열로 가지는 형태의 자료구조를 만들면 된다.

type Document struct {
    ID      int
    Content string
}

type InvertedIndex map[string][]int

func BuildInvertedIndex(documents []Document) InvertedIndex {
    index := make(InvertedIndex)

    for _, doc := range documents {
        tokens := strings.Fields(strings.ToLower(doc.Content))

        for _, token := range tokens {
            if _, ok := index[token]; !ok {
                index[token] = make([]int, 0)
            }
            index[token] = append(index[token], doc.ID)
        }
    }

    return index
}
type Document struct {
    ID      int
    Content string
}

type InvertedIndex map[string][]int

func BuildInvertedIndex(documents []Document) InvertedIndex {
    index := make(InvertedIndex)

    for _, doc := range documents {
        tokens := strings.Fields(strings.ToLower(doc.Content))

        for _, token := range tokens {
            if _, ok := index[token]; !ok {
                index[token] = make([]int, 0)
            }
            index[token] = append(index[token], doc.ID)
        }
    }

    return index
}

그리고 아래와 같이 역 인덱스를 생성할 수 있다.

func main() {
    documents := []Document{
        {ID: 0, Content: "apple favored chocolate"},
        {ID: 1, Content: "orange juice with candy"},
        {ID: 2, Content: "apple orange juice"},
    }

    index := BuildInvertedIndex(documents)
    for key, value := range index {
        fmt.Println(key, value)
    }
}
/*
output: 
with [1]
candy [1]
apple [0 2]
favored [0]
chocolate [0]
orange [1 2]
juice [1 2]
*/
func main() {
    documents := []Document{
        {ID: 0, Content: "apple favored chocolate"},
        {ID: 1, Content: "orange juice with candy"},
        {ID: 2, Content: "apple orange juice"},
    }

    index := BuildInvertedIndex(documents)
    for key, value := range index {
        fmt.Println(key, value)
    }
}
/*
output: 
with [1]
candy [1]
apple [0 2]
favored [0]
chocolate [0]
orange [1 2]
juice [1 2]
*/

문서의 우선순위 정하기

이제 우리는 주어진 쿼리로 원하는 문서를 빠르게 찾을 수 있다. 하지만, 원하는 쿼리가 포함된 검색 결과의 문서가 순서 없이 나온다면 그것은 품질이 좋은 검색 결과라고 보기 힘들다.

예를 들어 Merry Christmas, Mr. Lawrence라는 검색 결과가 있고 각 단어들이 포함된 문서들 중에 어떤 것이 사용자가 입력한 쿼리에 가장 가까울까? 즉 어떤 문서가 사용자가 입력한 쿼리에 가장 가까운지 순위를 매겨야 한다.

단순하게 우선순위 정하기

가장 단순하게는 쿼리에 포함된 단어가 많은 문서를 우선순위로 두는 것이다. 아래의 코드는 이를 구현한 예시이다.

func main() {
    documents := []Document{
        {ID: 0, Content: "apple favored chocolate"},
        {ID: 1, Content: "orange juice with candy"},
        {ID: 2, Content: "apple orange juice"},
    }
    index := BuildInvertedIndex(documents)
    query := "apple juice candy"
    tokens := strings.Fields(query)
    matchCount := make(map[int]int)
    
    for _, token := range tokens {
        if docs, ok := index[token]; ok {
            for _, docId := range docs {
                matchCount[docId]++
            }
        }
    }

    // ...
    // matchCount를 정렬한 뒤 문서 찾아서 반환하기
}
func main() {
    documents := []Document{
        {ID: 0, Content: "apple favored chocolate"},
        {ID: 1, Content: "orange juice with candy"},
        {ID: 2, Content: "apple orange juice"},
    }
    index := BuildInvertedIndex(documents)
    query := "apple juice candy"
    tokens := strings.Fields(query)
    matchCount := make(map[int]int)
    
    for _, token := range tokens {
        if docs, ok := index[token]; ok {
            for _, docId := range docs {
                matchCount[docId]++
            }
        }
    }

    // ...
    // matchCount를 정렬한 뒤 문서 찾아서 반환하기
}

하지만 이 방법 아래와 같은 문제가 있다.

  • 입력한 쿼리가 하나의 단어라면 이 방법은 의미가 없다.
  • 내가 입력한 단어가 포함된 문서가 많다면 이 방법은 의미가 없다.

즉 문서의 유사도만 고려할 뿐, 문서와 쿼리의 상관관계와 중요도를 고려하지 않는다. 이런 문제를 해결하기 위해 검색 엔진은 문서의 우선순위를 정하는 알고리즘을 사용한다. 대표적으로는 TF-IDF와 BM25가 있다. (앞의 FULLTEXT 인덱스 역시 이 두 알고리즘을 사용한다.)

TF-IDF

TF-IDF는 Term Frequency - Inverse Document Frequency의 약자로, 문서의 유사도를 계산하는 알고리즘이다. 여러 문서에서 자주 등장하는 단어는 중요도가 낮고, 특정 문서에서만 자주 등장하는 단어는 중요도가 높다고 판단한다.

TF-IDF의 계산식은 아래와 같이 표현할 수 있다. 이제 TF-IDF를 직접 구현해 보면서 어떻게 우선순위가 계산되는지 알아보자.

TFIDF=TF(d,t)×IDF(t)TFIDF = TF(d, t) \times IDF(t)

Term Frequency

Term Frequency는 문서에서 단어가 등장한 횟수를 의미한다. 구현은 간단하게 아래와 같이 할 수 있다.

tf := strings.Count(se.documents[docID].Content, token)
tf := strings.Count(se.documents[docID].Content, token)

역 문서 빈도 Inverse Document Frequency

Inverse Document Frequency는 단어가 전체 문서에서 단어가 등장하는 빈도(DF)를 고려하여 단어의 중요도를 계산하는 방법을 말한다

전체 문서 nn개가 있고, 단어 tt를 찾을 때 아래와 같이 계산한다.

DF(t)=DF(t) = 단어 tt가 등장한 문서의 수

IDF(t)=log(n1+DF(t))IDF(t) = log(\frac{n}{1+DF(t)})

n1+DF(t)\frac{n}{1+DF(t)} 식을 통해 문서 빈도에 전체 문서라는 역수를 취해 적은 문서에서만 등장하는 단어일수록 중요도가 높다고 계산하는 것을 알 수 있다. 여기서 분모에 1을 더해주는 이유는 단어가 어떤 문서에서도 등장하지 않는 경우에 분모가 0이 되는 것을 방지하기 위함이다.

또한 loglog를 취하는 경우는 문서의 수가 아주 많은 경우나 단어가 아주 적은 문서에서 등장하는 경우 값이 너무 과하게 커지는 것을 방지하기 위함이다. 이 IDF를 구현하면 아래와 같다.

tokens := strings.Fields(query)
scores := make(map[int]float64)

for _, token := range tokens {
    if matchedDocuments, ok := index[token]; ok {
        // Log(전체 문서 수 / 단어 token이 등장한 문서 수)
        idf := math.Log(float64(len(documents)) / float64(len(matchedDocuments)))
    // ...
    }
}
tokens := strings.Fields(query)
scores := make(map[int]float64)

for _, token := range tokens {
    if matchedDocuments, ok := index[token]; ok {
        // Log(전체 문서 수 / 단어 token이 등장한 문서 수)
        idf := math.Log(float64(len(documents)) / float64(len(matchedDocuments)))
    // ...
    }
}

TF-IDF 계산하기

TF와 IDF를 구하는 방법을 알았으니 TFIDF=TF(d,t)×IDF(t)TFIDF = TF(d, t) \times IDF(t)을 따라서 구현하면 된다. 이제 아래와 같이 문서의 점수를 계산할 수 있고 이 점수를 통해 문서의 우선순위를 정할 수 있다.

tokens := strings.Fields(query)
scores := make(map[int]float64)

for _, token := range tokens {
    if matchedDocuments, ok := index[token]; ok {
        // Log(전체 문서 수 / 단어 token이 등장한 문서 수)
        idf := math.Log(float64(len(documents)) / float64(len(matchedDocuments)))
        for _, docId := range matchedDocuments {
            tf := float64(strings.Count(documents[docId].Content, token))
            scores[docId] += tf * idf
        }
    }
}
tokens := strings.Fields(query)
scores := make(map[int]float64)

for _, token := range tokens {
    if matchedDocuments, ok := index[token]; ok {
        // Log(전체 문서 수 / 단어 token이 등장한 문서 수)
        idf := math.Log(float64(len(documents)) / float64(len(matchedDocuments)))
        for _, docId := range matchedDocuments {
            tf := float64(strings.Count(documents[docId].Content, token))
            scores[docId] += tf * idf
        }
    }
}

BM25

Best Matching 25 알고리즘은 TF-IDF의 단점을 보완한 알고리즘이다. TF-IDF는 문서의 길이를 고려하지 않기 때문에 아주 긴 문서에서 단어가 몇 번 등장하는 것과 짧은 문서에서 단어가 몇 번 등장하는 경우를 동일하게 처리한다. 이는 문서의 길이가 길어질수록 단어의 중요도가 떨어지는 것을 고려하지 않는다는 것이다. BM25는 이러한 문제를 해결하기 위해 문서의 길이를 고려하여 단어의 중요도를 계산한다.

식은 아래와 같이 복잡하게 생겼지만 TF-IDF와 크게 다르지 않다. 하나씩 살펴보면 아래와 같다.

QQ는 쿼리의 집합으로 Q1Q_1, Q2Q_2, ..., QnQ_n의 쿼리들이 있다.

k1k_1는 어떤 단어가 문서에 여러번 중요할 때 점수에 부스팅을 해주기 위한 파라미터 값으로 k1k_1가 클수록 단어의 중요도가 높아진다.

bb는 문서 길이를 얼마나 고려할지에 대한 파라미터 값으로 bb가 클수록 문서 길이를 더 많이 고려한다.

∣D∣|D|는 문서 DD의 길이를 뜻하고 avgdlavgdl은 전체 문서의 평균 길이를 뜻한다.

BM25(D,Q)=∑i=1nIDF(qi)⋅TF(qi,D)⋅(k1+1)TF(qi,D)+k1⋅(1−b+b⋅∣D∣avgdl) \text{BM25}(D,Q) = \sum_{i=1}^{n} \text{IDF}(q_i) \cdot \frac{TF(q_i, D) \cdot (k_1 + 1)}{TF(q_i, D) + k_1 \cdot (1 - b + b \cdot \frac{|D|}{\text{avgdl}})}

BM25 구현

tokens := strings.Fields(query)
scores := make(map[int]float64)

for _, token := range tokens {
    if docSet, ok := se.index[token]; ok {
        idf := math.Log(float64(len(se.documents)-len(docSet))+0.5) / (float64(len(docSet)) + 0.5)
        for _, docID := range docSet {
            tf := float64(strings.Count(strings.ToLower(se.documents[docID].Content), token))
            dl := float64(len(strings.Fields(strings.ToLower(se.documents[docID].Content))))
            numerator := (se.k1 + 1) * tf * (se.k1 + 1) / (tf + se.k1*(1.0-se.b+se.b*dl/se.avgDocLength))
            denominator := tf + se.k1*(1.0-se.b+se.b*dl/se.avgDocLength)
            scores[docID] += idf * numerator / denominator
        }
    }
}
tokens := strings.Fields(query)
scores := make(map[int]float64)

for _, token := range tokens {
    if docSet, ok := se.index[token]; ok {
        idf := math.Log(float64(len(se.documents)-len(docSet))+0.5) / (float64(len(docSet)) + 0.5)
        for _, docID := range docSet {
            tf := float64(strings.Count(strings.ToLower(se.documents[docID].Content), token))
            dl := float64(len(strings.Fields(strings.ToLower(se.documents[docID].Content))))
            numerator := (se.k1 + 1) * tf * (se.k1 + 1) / (tf + se.k1*(1.0-se.b+se.b*dl/se.avgDocLength))
            denominator := tf + se.k1*(1.0-se.b+se.b*dl/se.avgDocLength)
            scores[docID] += idf * numerator / denominator
        }
    }
}

테스트 해보기

type Document struct {
    ID      int
    Content string
    Score   float64
}

type InvertedIndex map[string][]int

type SearchEngine struct {
    index        InvertedIndex
    documents    []Document
    avgDocLength float64
    k1, b        float64
}

func (se *SearchEngine) Search(query string) []Document {
    tokens := strings.Fields(strings.ToLower(query))
    scores := se.CalculateBM25Score(tokens)

    var results []Document
    for docID, score := range scores {
        results = append(results, Document{ID: docID, Content: se.documents[docID].Content, Score: score})
    }
    sort.Slice(results, func(i, j int) bool {
        return results[i].Score > results[j].Score
    })
    if len(results) > 10 {
        results = results[:10]
    }
    return results
}

// 역 인덱스 및 BM25 구현 생략

func main() {
    documents := []Document{
        // ...
    }

    index := BuildInvertedIndex(documents)
    docLength := 0.
    for _, doc := range documents {
        docLength += float64(len(doc.Content))
    }
    searchEngine := SearchEngine{index: index, documents: documents, avgDocLength: docLength / float64(len(documents)), k1: 1.2, b: 0.75}

    for {
        fmt.Print("Enter a search query: ")
        query, _ := bufio.NewReader(os.Stdin).ReadString('\n')
        query = strings.TrimSpace(query)
        if query == "" {
            break
        }
        results := searchEngine.Search(query)
        fmt.Printf("%d results for query '%s':\n", len(results), query)
        for _, result := range results {
            fmt.Printf("- %s (score=%.2f)\n", result.Content, result.Score)
        }
    }
}
type Document struct {
    ID      int
    Content string
    Score   float64
}

type InvertedIndex map[string][]int

type SearchEngine struct {
    index        InvertedIndex
    documents    []Document
    avgDocLength float64
    k1, b        float64
}

func (se *SearchEngine) Search(query string) []Document {
    tokens := strings.Fields(strings.ToLower(query))
    scores := se.CalculateBM25Score(tokens)

    var results []Document
    for docID, score := range scores {
        results = append(results, Document{ID: docID, Content: se.documents[docID].Content, Score: score})
    }
    sort.Slice(results, func(i, j int) bool {
        return results[i].Score > results[j].Score
    })
    if len(results) > 10 {
        results = results[:10]
    }
    return results
}

// 역 인덱스 및 BM25 구현 생략

func main() {
    documents := []Document{
        // ...
    }

    index := BuildInvertedIndex(documents)
    docLength := 0.
    for _, doc := range documents {
        docLength += float64(len(doc.Content))
    }
    searchEngine := SearchEngine{index: index, documents: documents, avgDocLength: docLength / float64(len(documents)), k1: 1.2, b: 0.75}

    for {
        fmt.Print("Enter a search query: ")
        query, _ := bufio.NewReader(os.Stdin).ReadString('\n')
        query = strings.TrimSpace(query)
        if query == "" {
            break
        }
        results := searchEngine.Search(query)
        fmt.Printf("%d results for query '%s':\n", len(results), query)
        for _, result := range results {
            fmt.Printf("- %s (score=%.2f)\n", result.Content, result.Score)
        }
    }
}

적당한 문서 데이터를 넣고 검색을 해보면 아래와 같이 점수 계산을 통해 가장 유사한 문서가 상위에 노출되는 것을 확인할 수 있다.

8 results for query 'one day':
- All children, except one, grow up. They ...생략 (score=5.33)
- I have a dream that one day this nation ...생략 (score=3.69)
- I am an invisible man. No, I am not a ...생략 (score=3.28)
- It was a bright cold day in April, and ...생략 (score=2.05)
- It was the day my grandmother exploded. (score=2.05)
- As Gregor Samsa awoke one morning from ...생략 (score=1.64)
- The human race, to which so many of my ...생략 (score=1.64)
- When I consider how my light is spent ...생략 (score=1.64)
8 results for query 'one day':
- All children, except one, grow up. They ...생략 (score=5.33)
- I have a dream that one day this nation ...생략 (score=3.69)
- I am an invisible man. No, I am not a ...생략 (score=3.28)
- It was a bright cold day in April, and ...생략 (score=2.05)
- It was the day my grandmother exploded. (score=2.05)
- As Gregor Samsa awoke one morning from ...생략 (score=1.64)
- The human race, to which so many of my ...생략 (score=1.64)
- When I consider how my light is spent ...생략 (score=1.64)

정리

아주 기본적인 검색 기능 구현부터 시작해 데이터베이스를 활용한 방법과 역 인덱스를 구현하며 어떻게 검색에 용이한 구조로 데이터를 저장하는지, 그리고 TF-IDF와 BM25를 구현해 보며 검색 엔진에서 문서의 중요도를 어떻게 판별하는지에 대해 알아보았다.

하지만 이 글에서 구현한 검색 엔진은 Proof-of-work 수준의 기본적인 구현이며 아래와 같은 실제적인 문제점이 있다. 이 문제점들을 어떻게 해결하면 좋을지 고민하면 좋을 것 같다.

  • 모든 문서를 인 메모리에서 관리한다. 메모리는 비싸고 또 무한정 늘릴 수 없다. 어떻게 해야 할까?
  • 오래된 문서는 사실 검색을 할 때 잘 사용되지 않지만 종종 검색된다. 어떻게 관리해야 할까?
  • 실시간 검색어같이 자주 검색되는 단어는 어떻게 처리할까?
  • 검색어가 오타가 난 경우 어떻게 처리할까?
  • 문법적으로는 의미가 있지만 검색에서는 의미가 없는 불용어를 제거해야한다. (예: the, a, is, are)
  • 형태소 분석을 통한 자연스러운 검색을 지원해야한다.


이 글에서 작성된 검색 엔진 코드는 https://github.com/blurfx/mini-search-engine 에 공개되어있다.